I play a lot of pool/billiards, and under a lot of different rule sets. One of the formats I play is APA 9-ball rules. (Technically, now that I live in Japan, it's JPA, but the rules are the same as its parent American association.)
For a brief background of the rules, in 9-ball, you shoot the balls 1 through 9 sequentially in order, and typically the winner of a game is the player that pockets the 9 ball. APA rules changes the scoring of the game, where instead of winning 1 game point for each 9 ball pocketed, you win 1 point for each ball pocketed, and an extra point for pocketing the 9.
While playing a 9-ball match recently, I was the victim of a truly incredible streak of "rolls" by my opponent. (For non pool players, a "roll" is when you get lucky.) My opponent missed 11 times total in the match. 8 of those times I was totally snookered (no view of the object ball), and 1 time they fluked a ball in and continued their inning for a break and run. What this basically means is, I only had 2 capitalizable opportunities at the table following my opponent missing during the whole match.
I don't begrudge my opponent at all; they are a good player and a good person. It was an opportunity for me to try to exercise some stoicism in the face of misfortune. 🙃
⅔ of the way through the match, after watching another roll go by, I caught myself thinking "if this were a set match rather than APA rules, it would seem more winnable despite these rolls."
And that got me to thinking... It would be fun to create a simulation of two players playing 9-ball, add luck into the parameters, and see what effect the rules had on the results...
The simulation of luck in 9-ball
In my simulation (code here), there are two players: Alice and John. Alice is a better player than John, but they are both skill level 7s on the APA skill rating system. Alice is just a little bit more likely to put together strings of 5+ ball runs than John is.
In this twisted simulation world, Alice can never get lucky. Only John can get lucky. I define "getting lucky" as "that player gets another typical turn at the table." I think this is an accurate proxy implementation for "getting a roll". For example, safeing your opponent on a miss or fluking a ball in.
Each turn a player takes, they basically roll a weighted 10-sided die (marked with numbers 0 through 9). The number they roll indicates the amount of balls they run. The only difference is, after John misses, he gets to roll another die, and if he rolls high, he gets another turn.
Note that nothing in this simulation accounts for the differences in strategy between the games. Arguably, accounting for strategy differences would even further attenuate the effect of luck in set match rules, since the goal is not to take as many points as possible, the goal is to make the 9 ball, and a more skilled player would be better at crafting an executable plan to make the 9 ball. The point of this simulation is just to check what effect the rules difference has on the effects of luck.
The experiment
| Chance to run # balls in a single inning | John | Alice |
|---|---|---|
| 0 | 7% | 5% |
| 1 | 13% | 10% |
| 2 | 21% | 20% |
| 3 | 21% | 20% |
| 4 | 18% | 18% |
| 5 | 11% | 12% |
| 6 | 4% | 5% |
| 7 | 2% | 4% |
| 8 | 2% | 3% |
| 9 | 1% | 2% |
As you can see, Alice is just a little bit better than John. Alice has a 15% chance to make 1 or fewer balls, while John has a 20% chance of doing so. Alice has a 14% chance at running 6 or more balls, but John has a 9% chance. Small margins, but they add up over lots of matches.
Running the simulation
OK, let's have Alice and John play a million matches against each other and
we'll record the results. (To be exact, I simulated 131,072
matches across 8 different configurations, for a total of 1,048,576 simulated
matches of 9 ball.)
I had John and Alice alternate who starts the break (i.e. who wins the lag) for each match.
Zero luck (setting up ground truth)
| Rules format | Winning % for Alice |
|---|---|
| APA | 68.9% |
| Set match race to 5 | 57% |
With no luck involved, Alice wins 69% of the time (nice!) in APA, and 57% of the time in the set match (race to five).
Adding luck
| Rules | Alice Win % (20% luck) | (40% luck) | (50% luck) |
|---|---|---|---|
| APA | 34% | 9% | 3% |
| Set match | 43% | 27% | 19% |
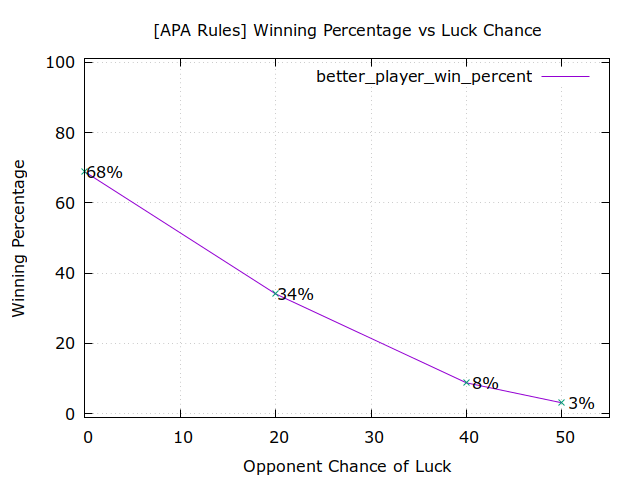
As you can see, with only 20% luck (every five shots, John gets a roll) Alice's
69% APA winning chance is already cut in half to 34% and she's a big underdog!
At 50% luck (every other miss, John gets a roll), Alice only wins 3% of
131,072 matches!
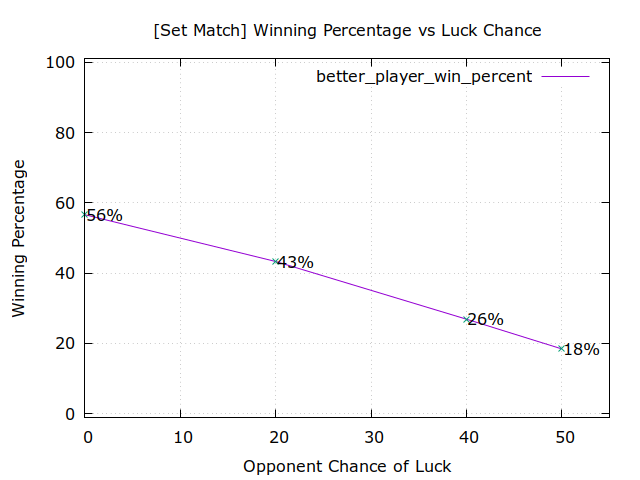
In contrast to the APA rules, even with a 50% luck rate for John, Alice still manages to take about ⅕ of the race to five set matches. In a set match, Alice's winning rate reduces linearly with the amount of luck John gets, but in APA her winning rate reduces geometrically. Basically, if your opponent is getting a bunch of rolls, you'd rather be playing a set match.
Getting rolls
Now, you might say "OK, but it's not that realistic for your opponent to get lucky 20-50% of the time", but APA skill level 7s, 8s, and 9s only really miss a handful of balls a match. So the variance is high — they only need a couple of rolls on those few misses to edge out their opponent, even if they're technically outclassed.
Another point worth mentioning is, when you get a roll, you also get another chance at getting a roll. Because getting a roll means getting back to the table in a favorable position, you essentially get a free roll at another roll. So you're not only gaining points but you gained another chance at rolling the die on getting lucky again.
Intuition for set matches being less affected by luck
In a set match, if you get a roll, that roll only matters it if contributes to you pocketing the 9 ball. On the other hand, every roll you get under APA 9 ball rules contributes to your winning chances (in an amortized sense) because you can model an expected number of points per inning at the table.
Wrap up
When your opponent is getting lucky every other shot in APA, and it feels like you can't win... don't despair! Under those conditions, statistically speaking, you should lose 97% of the time!
And all of this is to say nothing of the human element: that we tend to play worse when nothing is going our way. But we need to work hard to be stoic under pressure when we're at the mercy of bad luck, because the odds are ever-so stacked against us.